Copyright © Had2Know 2010-2024. All Rights Reserved.
Terms of Use | Privacy Policy | Contact
Site Design by E. Emerson
Silver Ratio Calculator
The silver ratio is an analog of the more well-known golden ratio. A silver rectangle has an aspect ratio of 1:1+√2, or approximately 1:2.41421356. The number 1 + √2 is not called the silver constant or silver number, as those terms are reserved for other numbers. The silver ratio is usually represented by the symbol δs.
The silver ratio arises in many mathematical and geometric expressions. For example, the continued fraction

converges to δs. The continued radicals

and
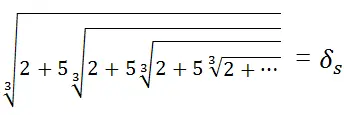
also converge to δs. These arithmetic expressions can be resolved by solving the equations
x = 2 + 1/x, x = √1+2x, and x = ∛2+5x.
The silver ratio also appears as the limiting ratio of solutions to the Pell equation 2x² ± 1 = y² For instance, the first several solution pairs are
(1, 1) 2x² - 1 = y²
(2, 3) 2x² + 1 = y²
(5, 7) 2x² - 1 = y²
(12, 17) 2x² + 1 = y²
(29, 41) 2x² - 1 = y²
(70, 99) 2x² + 1 = y²
(169, 239) 2x² - 1 = y²
(408, 577) 2x² + 1 = y²
⋮
If you take the ratio of consecutive y terms, you obtain
3/1 = 3
7/3 = 2.3
17/7 = 2.428571
41/17 = 2.411765
99/41 = 2.414634
239/99 = 2.41
577/239 = 2.414226
As you can see, the ratio converges to 1 + √2. You will also see the same pattern if you take the ratio of consecutive x terms.
To understand δs geometrically, suppose you have a rectangle whose sides are in a ratio of 1:δs. When you cut two perfect squares from the rectangle, the remaining rectangle is also a silver rectangle. If you repeat the process over and over, you obtain the pattern shown on the left:

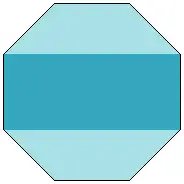
width = length/δs
length = width × δs
© Had2Know 2010
