Copyright © Had2Know 2010-2024. All Rights Reserved.
Terms of Use | Privacy Policy | Contact
Site Design by E. Emerson
Constructing Geometric Solids:
Rhombic Dodecahedron
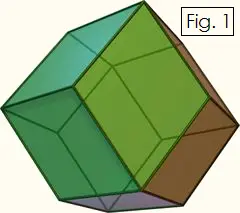
A rhombic dodecahedron is a 12-sided solid shape in which every face is a rhombus, i.e., a quadrilateral with four sides of equal length, a diamond. One interesting property of rhombic dodecahedrons is that you can create a 3-dimensional tessellation with them, that is, you can pack them together with no gaps, just as you can do with cubes. The rhombic dodecahedron is also the dual of the cuboctahedron, since each vertex of the rhombic dodecahedron corresponds to a face of the cuboctahedron, and vice versa.
You can construct rhombic dodecahedrons out of stiff paper and glue (or clear tape) using the pattern and instructions that follow below. You will also need a ruler, pencil, and sharp scissors or an Xacto knife.

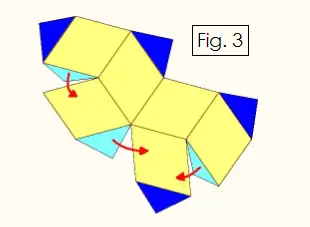
Using a ruler, sharp pencil, and the rhombus pattern in Figure 2, draw two copies of Figure 3 below. For each of these two of these figures, fold upward along every edge, and glue the light blue tabs onto the yellow rhombuses as indicated by the red arrows. You will then have two cup-like halves.
Once the glue on your solid shape has dried, you are done! Make several rhombic dodecahedrons and stack them like cubes without creating any gaps. You can also use these polyhedra as 12-sided dice.
© Had2Know 2010
